About Confusion Example
Alice's and Bob's example
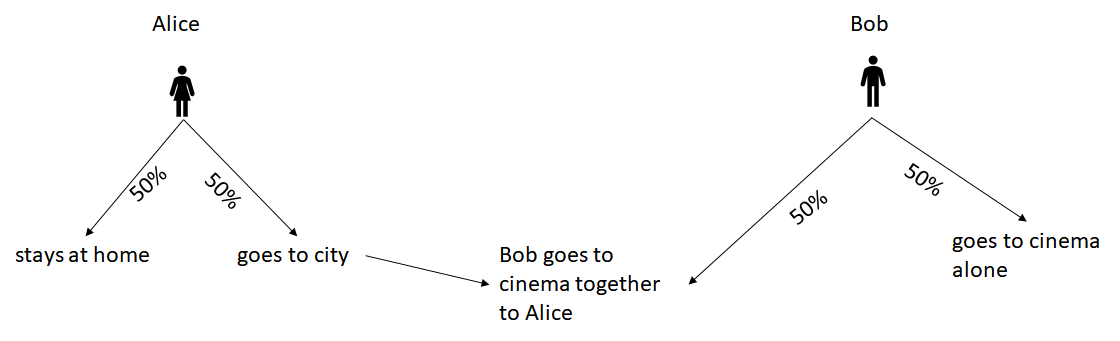
Suppose that a concurrent and probabilistic system is composed by two agents: Alice and Bob.
Alice has to decide whether to go to city (50% of probability) or to stay at home (50% of probability).
Bob has to decide whether to go to theater alone (50% of probability) or with Alice (50% of probability). But this last option is only possible if she chooses to come to the city.
Alice's and Bob's example in Petri Net
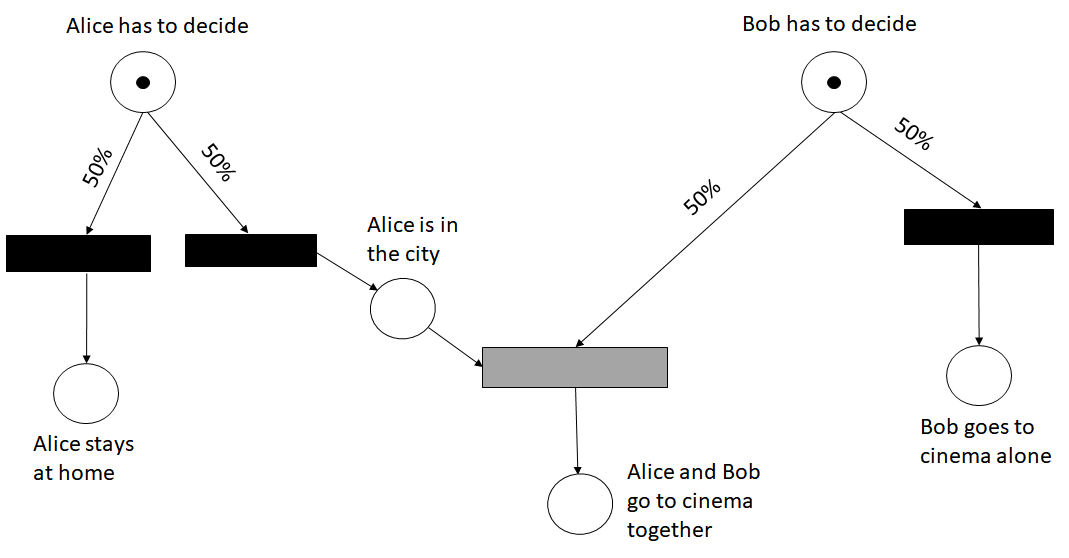
The Alice's and Bob's example can be represented through Petri nets.
The initial state of the system in which Alice and Bob have made no decision yet is represented by tokens in the places Alice has to decide and Bob has to decide
The choices of Alice are represented by transitions that consume tokens from the place Alice has to decide,
while the choices of Bob are represented by transitions that consume tokens from the place Bob has to decide
Initially the transition representing the decision of Bob to go to cinema together to Alice is not enabled since Alice isn't in the city (no token in the place Alice is in the city)
Therefore, at the moment, Bob has the only possibility to go to cinema alone
Alice decides to go to city
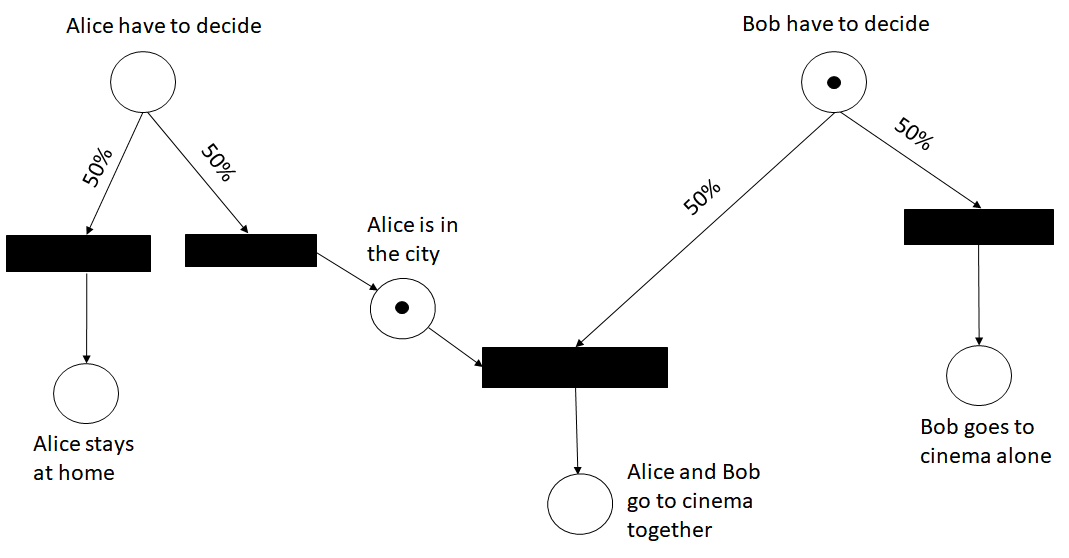
After Alice decides to go to the city (a token reaches the place Alice is in city), the transition that represents the decision of Bob to go to cinema together to Alice is enabled.
Now Bob has all the options available, then he has 50% of probability both to decide to go to cinema alone and to decide to go to cinema together
Concurrent process
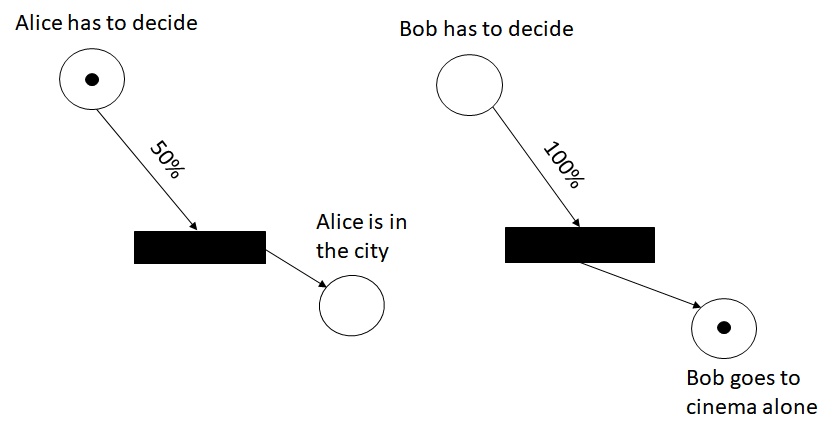
Situation #1
Bob decides before Alice
IIn this situation first Bob decides to go to the cinema alone. This choice is taken with 100% of probability since it is the only option for Bob. This situation finishes with Alice that decides to go to the city. The latter choice is taken with 50% of probability

Situation #2
Alice decides before Bob
In this situation first Alice decides to go to the city. Therefore Bob has all options available since now he can invite Alice to go to cinema together. Bob has 50% of probability to choose either to go to the cinema alone or to go there with Alice. The situation finishes with Bob that decides to go to the cinema alone.
Confusion problem
situation#1 and situation#2 correspond to the same concurrent process from the concurrency point of view, but they have different probabilities to be executed. Therefore, there is some confusion about the assignment of the right probability to this concurrent process.